Writing a Simple Chess-Engine in C++

Originally published on LinkedIn on July 8, 2020

Something that was unfortunately lost in time is a chess program I had originally written many years ago in Pascal. The program implemented the rules of chess and also allowed the player to challenge a computer opponent. Out of nostalgia, I redid this project last year and used the opportunity to familiarize myself more with C++.

The result is very crude (by virtue of the facts that I am a complete chess novice and that several improvements to the codebase can be made), but it was nonetheless a fun little project I would like to share. The entire code is available on GitHub, and its general principles shall be covered here without going into too much detail.

The article is aimed at readers who have no familiarity with computer chess whatsoever. Readers with a deep knowledge of coding and/or chess will likely not be exposed to new information here and could instead look at excellent, much more advanced resources, e.g. Gamechanger or - for more classical algorithms - the architecture of Stockfish.

The Interface

As most things in the coding space do, the chess engine started as a command line based program. The chess board is simply displayed via characters on the console, with background coloring to aid in distinguishing the pieces. The algorithm to draw the board is straightforward: Iterate through the board and write characters to the console depending on which piece is present. Text-based command line inputs are taken to e.g. move pieces, reset the board, or make the engine perform a move:

This is clearly neither aesthetically appealing, nor user friendly - so the natural next step is to think of a proper way of interfacing with the user. Still, the code for the original command line based version is on GitHub for reference.

Now, this initially struck me as an terrifying task, since I have always thought of graphical user interfaces as being extremely cumbersome to deal with in C++. Thankfully, there are wonderful libraries such as wxWidgets and I came across a great tutorial on the same.

This is what the outcome looks like.
The process of implementing a GUI is not as simple as it was several years ago when I used Delphi (which was pretty much a drag-and-drop sandbox for GUI programming). However, the basic principle is still pretty intuitive: Create objects representing UI elements and then define event handlers for them.
To enable interaction with the chess pieces, the program uses an OnClick-event on the chess board and a state machine would take care of the rest. For example, if a piece had already been selected and an empty square is clicked, it is checked whether this represents a legal move, and if it does, it is executed (we'll get to the actual rules of the game in a bit).

Now, chess programs are dime a dozen on the internet, so I am happy to give a shoutout to Kimberley for designing these neat pieces for me and giving the program a more unique touch:

Initial Caveats on Representation of the Board and its Pieces

The board representation is the principal prerequisite of any engine. How do you encode the chess board and it's pieces? The answer to these questions dictates how moves are generated and executed, and hence massively influences the performance of any engine (which has to cycle through millions of moves to find one it deems optimal).

Now, modern, strong engines use bitboards, which essentially represents the board as a set of 64-bit integers (8x8 bits), where a "1" would indicate that a piece is present, and a "0" would indicate the opposite. Move generation and execution can hence be handled via sequences of extremely fast bitwise operations (AND, OR, NOT, XOR, et cetera) which are executed within the CPU registers directly, requiring few clock cycles and low memory delays. The goal is to minimize the clock cycles per move and hence maximize the considered moves per second. Several grid based games are amenable to this approach, Connect 4 being one example I may cover at another time.

Here, I followed a much simpler and less efficient, but more readily understandable approach in the context of Object Oriented Programming: Namely, the idea is to represent the objects of the game, i.e. pieces and the board itself, as classes whose instances are stored in memory.

The Pieces

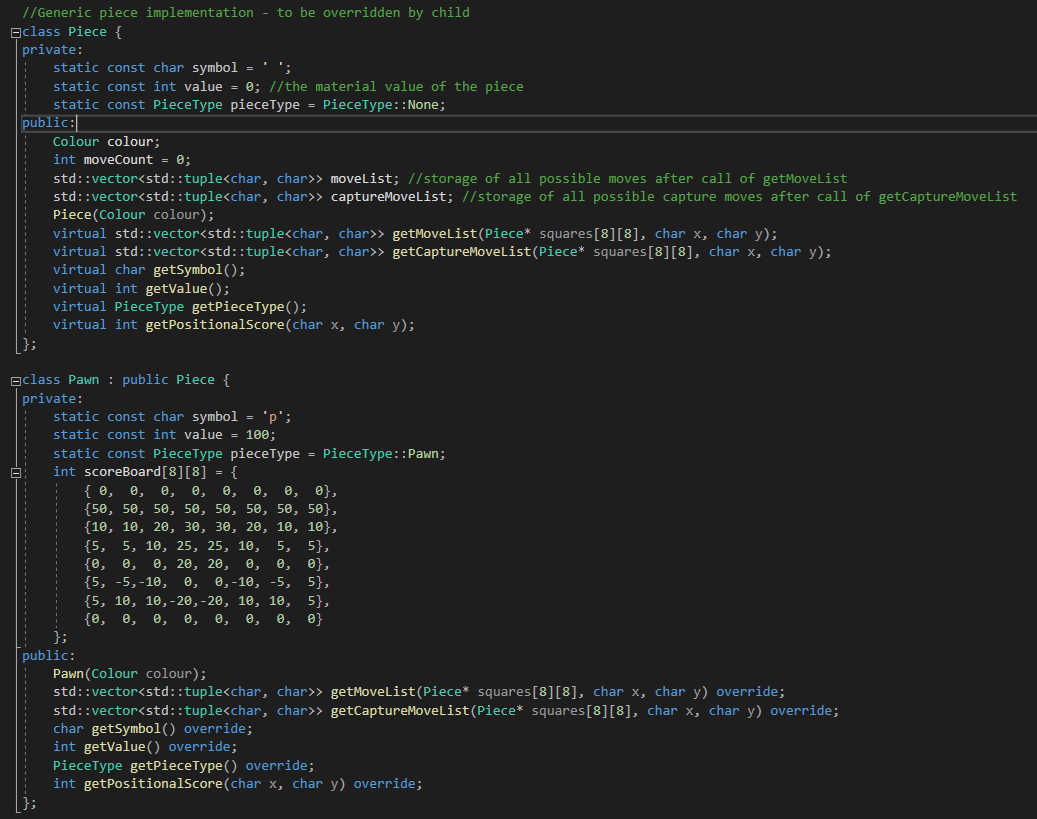
For each chess piece, a class is written which encodes e.g.:

The piece's material value (integer)
The piece's positional value (integer)
The move generation routine (a method that encodes the move-rules for each piece, e.g. the horizontal and vertical sliding for rooks)
The colour (an enum type, black/white).

Hence, we have the following classes: Pawn, Knight, Bishop, Rook, Queen, Knight - as well as a "generic" Piece-class from which all of these are inherited. The chess board is hence declared as an 8x8-Array containing pointers to this generic Piece (and not a Pawn, Bishop etc. directly).

Sidenote. Why have a generic parent class? The reason is the practicality that comes from polymorphism in C++. Imagine that we want to look at a certain square on the chess board and generate all possible moves for the piece on that square. We do not need to perform explicit checks on which piece is present on the square when we do this; Instead, the code will just invoke the (virtual) move generation routine of the generic Piece, which during runtime is actually a concrete piece in heap-allocated memory. This concept of polymorphism allows us to keep the code relatively succinct. Remember that a virtual method is one which is essentially declared as a placeholder, a method whose definition depends on derived child classes. See this StackOverflow post for another instructive example.

The below excerpt shows some of the class declarations in pieces.h:

Each piece can generate a set of quasilegal moves given the current chess board state which is implemented differently for each piece type. Moreover, only those moves resulting in a capture of an opponents piece can be generated, for reasons that will become clear in a bit when we cover quiescence searches. Quasilegal moves are defined as those within the move rules of the piece, disregarding for now whether the player would e.g. check himself by executing the move (ie. checks are disregarded which require knowing the broader game state - those are delegated to the chess board).

N.B. upon re-reading the above declarations, some improvements come to mind- if the class already stores a list of moves, I should have just returned pointers to the same in getMoveList and getCaptureMoveList for additional efficiency.

What is the point of storing a material- and positional value (see the matrix in the above code snippet)? These are features of the engine: Each piece has a material value and a scoreBoard, the latter of which dictates how much "extra" a piece is worth depending on it's location. In the case of a white pawn, being near the opposite end is advantageous because it increases the likelihood of a successful promotion, and controlling the center is also attached with a positive bias. This will be meaningful when we try to attribute a numerical value to a chosen move in an attempt to quantify how good it is.

The Board

As noted above, the chess board is an 8x8-array of pointers, pointing to either nullptr if no piece is present, or to the instance of one of the pieces.

The key responsibility of the board is to execute a move (checking whether it is legal before doing so!) and providing the means for undoing a move. To facilitate this, each executed move is stored in a struct, containing the essential information (e.g. whether the move was a castling, or an en passant capture, whether the previous move allowed for an en passant). The reason is this: For the engine to traverse a certain set of potential moves downward, it will be required to fully restore the game state when the search tree is traversed back up.

I won't go into detail on the move-routines here, but feel free to reach out to me if you're interested. It takes as input a source coordinate and a target coordinate, and from there it's basically a blunt implementation of the chess rules, going through applicable checks as needed: If the move attempts a castling, it checks that the relevant squares are not attacked by the opponent, that both the king and rook haven't moved yet, et cetera. There is not much in terms of interesting concepts here.

The Engine: The Tree of Possible Moves

There are many different algorithms to tackle the problem of determining an optimal move. At the most naïve level, you might recognize that the possible future game states are encoded by a tree, where each node represents the board and each edge represents a move, and then you might try the following:

Cycle through all possible pieces on the board for the player whose turn it is
For each piece, generate all legal moves
Check if the move results in a checkmate. If it does, the game is won, and that move is optimal and returned by the function. If it does not, the move is executed and step 1. is called again with the opposing player (i.e. the depth is increased by one).

Clearly, for a game like Chess, this will not work - the theoretical reason being that there are infinite move chains, if one does not include a rule that the game ends in a draw after e.g. N moves without any capture. The algorithm would endlessly go down certain branches. The practical, and much more constrictive reason, is that the game is too complex for arbitrary depth. See also the article on wikipedia on game complexity. In simple terms, the move tree just explodes in size after just a few turns.

Contrast this with a solved game like Tic-Tac-Toe which is guaranteed to end after a finite (and small) number of turns - you could simply apply brute force to compute the entire move tree.

Hence, the first insight is that we need to stop after a certain number of turns, i.e. we prune the depth of the searched tree. Clearly, this results in the next problem: The end state will generally not be a checkmate, stalemate or draw, meaning that we need a heuristic algorithm evaluating the game state.

The Engine: Evaluation Functions

Aside from technicalities on how the tree is traversed, the evaluation function is arguably the "meat" of the engine, and the point at which the most chess expertise would come into play. Without looking any turns into the future, how "good" do we think that a given position is?

The algorithm utilized here works along three straightforward steps:

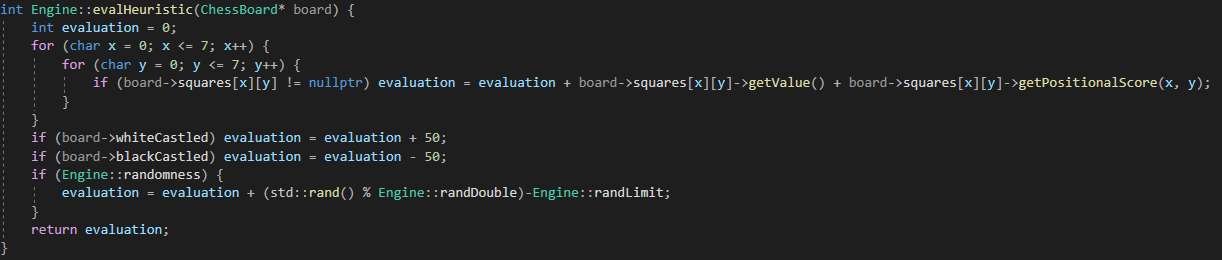
Sum up the material on the board. As noted in the code snippet on the Chess pieces, a Pawn is e.g. allocated a numerical value of 100 for white and -100 for black. So, we can simply add these numbers up; a positive number is good for white, a negative number is good for black. The king is assigned a large number in absolute terms to incentivize attempts to capture it.
Evaluate the positional strength of each individual piece. This was also alluded to in the aforementioned code snippet, where it was noted that a pawn close to the opposite end of the board is worth much more by virtue of increasing the likelihood of a pawn promotion. A more in-depth article can be found here.
A positive bias is added for castling.

There are a lot more strategic adjustments that can be made, and modern engines like Stockfish have much more complicated evaluation functions. It should be noted, for example, that static positional strength matrices are less than optimal: For example, the assumption that a king hiding in the starting row is a good thing only holds true in the early stages in the game, whereas it could be used more offensively in later stages.

In code:

The algorithm also adds, if desired, a random quantity to avoid the game playing out the exact same way under a given searched depth.

The Engine: Searching (and Pruning) the Move Tree

To summarize, the idea is to search the position tree up to a given depth, calculate the heuristic value of each end state, choosing the move that results in the largest value for white (and the smallest value for black) - and returning the best value from each perspective back up the tree.

This is formalized by the Minimax algorithm and illustrated nicely in pictures under the previous link. We already noted that we prune the tree depth for practical reasons - but is there a way to further cut off branches without affecting the end result?

From the Wikipedia article on the Alpha Beta algorithm:

[...] suppose somebody is playing chess, and it is their turn. Move "A" will improve the player's position. The player continues to look for moves to make sure a better one hasn't been missed. Move "B" is also a good move, but the player then realizes that it will allow the opponent to force checkmate in two moves. Thus, other outcomes from playing move B no longer need to be considered since the opponent can force a win. The maximum score that the opponent could force after move "B" is negative infinity: a loss for the player. This is less than the minimum position that was previously found; move "A" does not result in a forced loss in two moves.

In general terms, we can retain the minimum value that the maximizing player is currently assured of, alpha, and the maximum value that the minimizing player is assured of, beta. If these values are updated and alpha<=beta no longer holds true, i.e. we have alpha > beta, we can stop the search at this branch because rational players would not end up here.

This is a major gain in performance. I won't expand much more on this pruning concept here because there are ubiquitous articles and examples - the key takeaway is that this is a simple and effective method of reducing the traversed nodes.

The Engine: Quiescence Searches

Another very natural concept is to make moves that result in a "quiet" position where no more captures can be made. Think of the following scenario: The tree is searched up to depth 4, and the last move results in the queen capturing a rook. This might look like a very good move on paper. However, what if - in the next move - the queen is captured? That would likely be a bad deal, and is one example of the Horizon Effect.

Hence, what we can do is - after we have reached the maximum depth we want to consider - look at additional, further moves that just result in pieces being captured. There are other ways of mitigating the risk of bad deals at the search horizon, this one being quite straightforward.

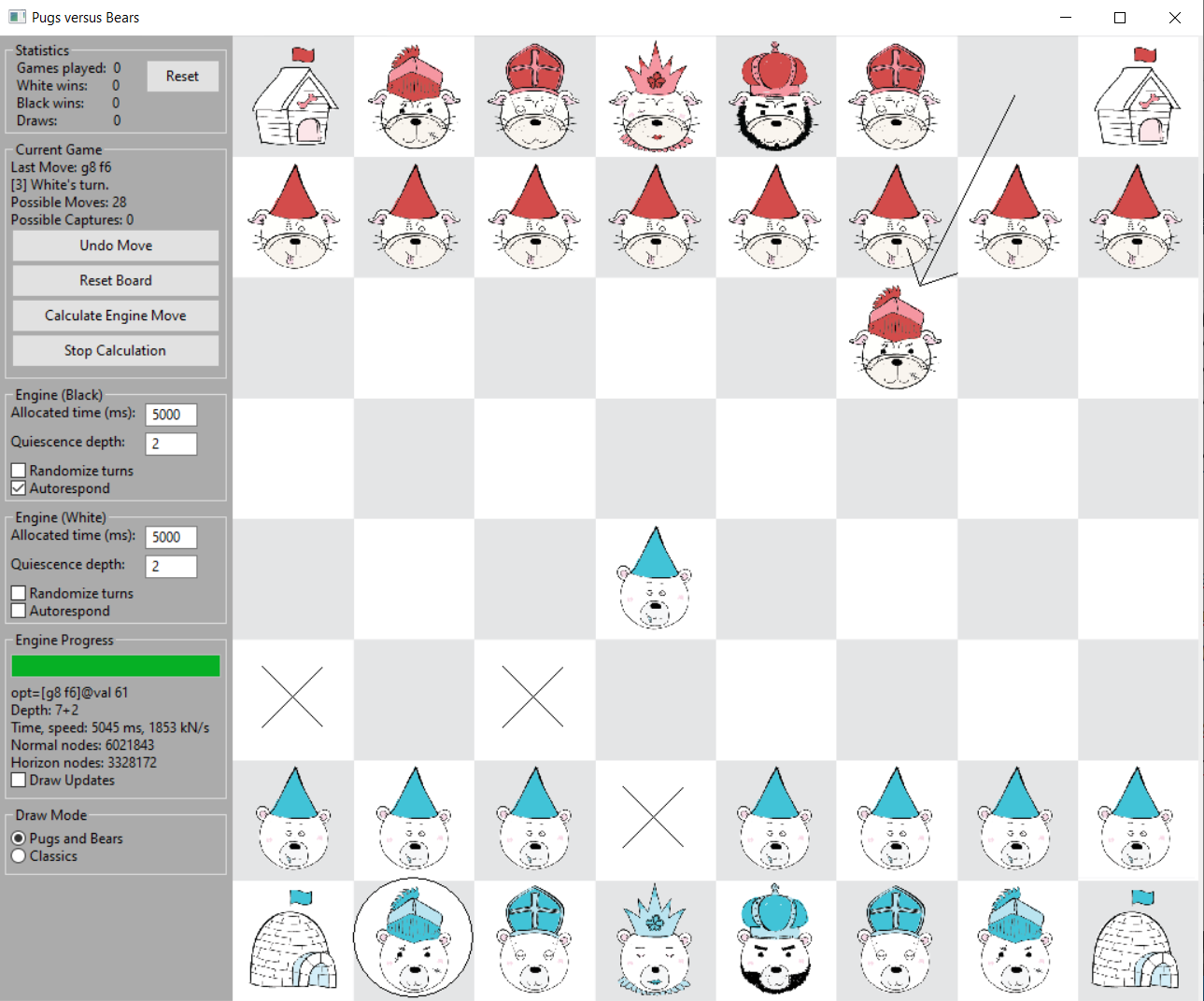
A practical constraint is that - because we go further down the tree - there are many capture moves to consider. See the below example, where the last move of black was calculated:

Quiescence Search

There were about 360.000 normal nodes visited, versus over 8 million nodes at the horizon. The runtime is dominated by quiescence searches unless we restrict the time spent on quiescence searches. In practice, the quiescence search can be cut off after a fixed additional depth, e.g. 2 in the above case for white.

The Engine: Iterative Deepening

So far, we have covered the engine in terms of a fixed search depth. However, in the above screenshot, you may notice that we allocate a fixed time to the engine. The reason for this approach is that the calculation complexity is a function of the current game state: For instance, a depth of 5 at the beginning is calculated much quicker than a depth of 5 later in the game, especially as sliding pieces (rooks, queens, bishops) have a lot more possible moves at their disposal. Consequently, an approach is needed to keep the runtime manageable.

One such algorithm is given by iterative deepening, which starts with depth 1 and subsequently increases the depth as long as it stays within the allocated time. If the time constraint is violated, the best move from the last completed search is used. This might seem wasteful, but keep in mind that:

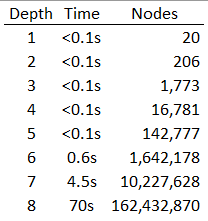
The search tree grows exponentially. This means that, if a given depth suddenly takes very long to traverse, the previous maximum depth is quite likely searched much faster. Below is an illustration of the search complexity from a given starting position, where it is notable that the cumulative time for all individual searches from depth 1 to depth 6 requires only about 7% of the time it takes to do a depth-8 search:

We pass the previously found best move to the next iteration, i.e. if a given move was optimal for depth N, the depth N+1 search starts with this move first. Recall the above section on Alpha Beta pruning: This should ideally lead to a lot of pruned branches. The intuition is that the previous result is a best guess on what we should try next. For example, if we were to start a depth 8 search with the result from the depth 7 search, the visited nodes are reduced from about 162 million to 130 million, i.e. by 20%. Hence, the time spent on prior depth searches is not wasted.

N.B. The above numbers are highly dependent on the random quantities used by the evaluation function and the pruning algorithm. For a stable and precise computation of the actual nodes, a Perft analysis should be performed.

Conclusion

This was a very brief illustration of a simple chess program could be structured. There are plenty of improvements to make, some of which we mentioned before:

Hashtables. There are different turn sequences resulting in the same intermediate position, and if such an already-visited position is found, we do not need to look further - the result has already been calculated. This can be implemented by attaching a hash key to each position and storing search results in a large array indexed by these keys.
Opening tables. There are known good responses to certain openings, and by leveraging such a database, the initial moves of the engine can be improved upon.
A better evaluation function. Dynamic scoreboards and scanning for certain advantageous positions - this is where a lot more Chess theory would come into play.
Better tree pruning. See for example Killer Heuristics.
Faster move generation. For instance, by replacing the Object Oriented Board representation with Bitboards.

... And many more, some less straightforward than others.

Perhaps this project will be continued in the future along some of these lines, but for now, this is it. I hope you enjoyed this little excursion!